游戏攻略
我的起源怎么捕捉毒鳄龙-毒鳄龙弱点属性捕捉方式介绍
2019-12-10 10:55:58 阅读(98)
我的起源是一款以生存创造、复苏世界文明为主题的热门手机游戏,游戏中有很多的宠物,每一个宠物都是有自己的特点和捕捉方法,今天就给大家带来我的起源毒鳄龙弱点属性捕捉方式介绍,感兴趣的小伙伴快来看看吧。
我的起源毒鳄龙

分为:毒鳄龙、疯狂的毒鳄龙、变异的毒鳄龙、数据毒鳄龙
【详情】
名称:毒鳄龙
定位:近战输出
所属时代:星历300年
弱点属性:穿刺伤害/冰元素
攻击属性:穿刺伤害/毒元素
【技能】
骑乘技能:毒鳄龙急速滚动撞击敌人,造成伤害和击飞效果。滚动时自身免疫控制,移动速度提升
普攻技能:用利齿攻击敌人,造成单体伤害
【击败可获得】
兽腿肉、沁毒龙牙
毒鳄龙

毒鳄龙经常隐藏在危险的沼泽中,在猎物放松警惕时迅速用利齿与毒液给予致命一击。是凶猛的近战输出宠物。
[收集属性]
生命值:+30
命中值:+1
激活条件:装备一只以激活收集属性
[额外收集属性]
闪避值:+1
激活条件:装备一只资质达到1400的以激活收集属性
疯狂的毒鳄龙

虽然在外表上与其他的毒鳄龙没有太大的差别,但是这些毒鳄龙是更为可怕的捕食者
[收集属性]
生命值:+148
命中值:+6
激活条件:装备一只疯狂的毒鳄龙以激活收集属性
[额外收集属性]
闪避值:+6
激活条件:装备一只资质达到1800的疯狂的毒鳄龙以激活收集属性
变异的毒鳄龙

这是一只被星神气息所污染的毒鳄龙,它有着极强的战斗欲望,在每一次战斗时都会全力以赴,在它眼中,任何对手都不过是羔羊
[收集属性]
生命值:+222
命中值:+9
激活条件:装备一只变异的毒鳄龙以激活收集属性
[额外收集属性]
闪避值:+9
激活条件:装备一只资质达到2200的变异的毒鳄龙以激活收集属性
数据毒鳄龙

数据毒鳄龙是被以太数据化的毒鳄龙,它们的实力被以太大大加强,有着极强的侵略与攻击型,是探寻者们喜爱的宠物之一
[收集属性]
生命值:+333
命中值:+13
激活条件:装备一只数据毒鳄龙以激活收集属性
[额外收集属性]
闪避值:+13
激活条件:装备一只资质达到2500的数据毒鳄龙以激活收集属性
获得方法
在星历218年的原罪之岛捕捉可获得。
毒鳄龙:捕捉毒鳄龙获得
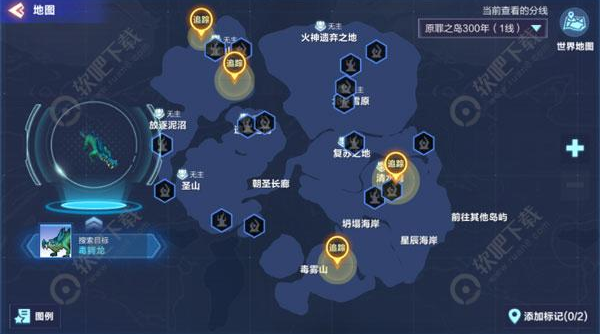
疯狂的毒鳄龙:有几率遇到
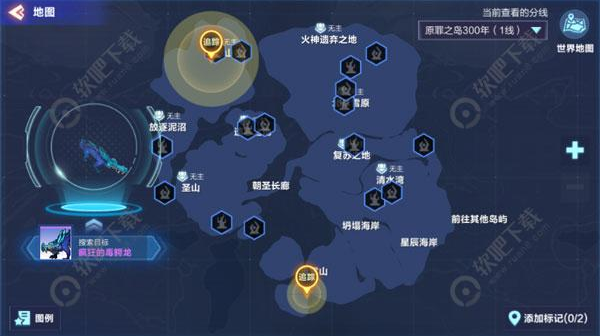
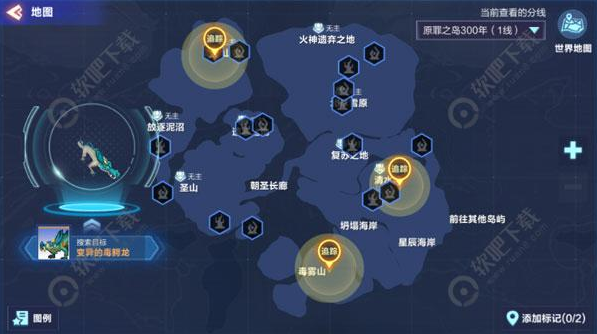
变异的毒鳄龙:有几率遇到
以上全部内容,由Jw游戏网小编小奶瓶为您提供,更多精彩游戏资讯关注《我的起源》专区,每天为你带来最新消息!
| 我的起源宠物图鉴大全 | |||
|---|---|---|---|
| 加姆犬 | 金猪 | 严风兽 | 数据金猪 |
| 疯狂加姆犬 | 变异严风兽 | 疯狂严风兽 | 变异加姆犬 |
| 数据伞蜥龙 | 数据毒鳄龙 | 红颈企鹅王 | 剑齿虎 |
| 鬣狗 | 墨水斑马 | 毒鳄龙 | 高地熊 |
| 伞蜥龙 | 疯狂的鬣狗 | 疯狂剑齿虎 | 疯狂毒鳄龙 |
| 疯狂高地熊 | 疯狂伞蜥龙 | 变异的鬣狗 | 变异剑齿虎 |
| 变异毒鳄龙 | 变异高地熊 | 变异羽迅龙 | 变异伞蜥龙 |
| 变异墨水斑马 | |||
| 近战坦克宠物 | |||
| 甲龙 | 疯狂的甲龙 | 变异的甲龙 | 冰石蟹 |
| 疯狂冰石蟹 | 变异冰石蟹 | 蛮足龙 | 数据熔石蟹 |
| 数据猛犸 | 数据电刺猬 | 雕齿兽 | 雷犀 |
| 铲齿象 | 布莉姆温 | 疯狂铲齿象 | 变异的雷犀 |
| 变异雕齿兽 | 变异铲齿象 | ||
| 远程输出宠物 | |||
| 大角鹿 | 疯狂大角鹿 | 变异大角鹿 | 枭羽龙 |
| 猎影枭羽龙 | 数据大角鹿 | 数据火蝙蝠 | 数据恐鸟 |
| 雷神古树 | 变异枭羽龙 | 恐鸟 | 焰火鸟 |
| 疯狂的恐鸟 | 疯狂焰火鸟 | 变异的恐鸟 | 变异焰火鸟 |
| 枯萎巨龙 | |||
| 治疗辅助宠物 | |||
| 水栖兽 | 疯狂水栖兽 | 变异水栖兽 | 数据水栖兽 |
| 数据地懒 | 数据冰狐狸 | 沼栖兽 | 雪地大角鹿 |
| 疯狂沼栖兽 | 疯狂雪地鹿 | 变异沼栖兽 | 变异雪地鹿 |
| 树枫龙 | |||
| 点击此处返回我的起源全攻略汇总 | |||
相关推荐
-

我的起源宠物有哪些-我的起源宠物属性特点图鉴汇总
2019-12-10
-

我的起源怎么捕捉树枫龙-树枫龙弱点属性捕捉方式介绍
2019-12-10
-

我的起源怎么捕捉变异的雪地大角鹿-变异的雪地大角鹿弱点属性捕捉方式介绍
2019-12-10
-

我的起源怎么捕捉变异的沼栖兽-变异的沼栖兽弱点属性捕捉方式介绍
2019-12-10
-

我的起源怎么捕捉疯狂的雪地大角鹿-疯狂的雪地大角鹿弱点属性捕捉方式介绍
2019-12-10
-

我的起源怎么捕捉疯狂的沼栖兽-疯狂的沼栖兽弱点属性捕捉方式介绍
2019-12-10
-

我的起源怎么捕捉雪地大角鹿-雪地大角鹿弱点属性捕捉方式介绍
2019-12-10
-

我的起源怎么捕捉沼栖兽-沼栖兽弱点属性捕捉方式介绍
2019-12-10
-

我的起源怎么捕捉数据冰狐狸-数据冰狐狸弱点属性捕捉方式介绍
2019-12-10
-

我的起源怎么捕捉数据地懒-数据地懒弱点属性捕捉方式介绍
2019-12-10






















































































